My Math Clock

Posted on May 25, 2009 by Iceman

Absolutely arbit post ….. I am doing an intern in Zeus Numerix in Pune again this summer and am working on some really interesting stuff . All throughout the day I am generally in front of the PC studying ebooks and writing in C/C++. A change would have been kinda nice … I decided to make a clock except that all the numbers would be represented by their mathematical significance …..(Just to get some experience on woodwork ,etc. ….. 😛 ) I got the mechanism for the clock from a local watch maker . For the base I decided to use wood from an old unwanted cupboard . A hacksaw , hammer were good enough to cut a piece approximately 18cm x 14cm x 1cm . To drill a hole so that the mechanism could be put in place I visited our electrician . To smoothen the surfaces I used a sand paper lying around my house .For the layout of the clock i.e. the numbers etc. I used Scribus along with $\LaTeX$ .

Finally the layout or background looked like this ….. I did also add a $t$ denoting for the time variable …. 😉

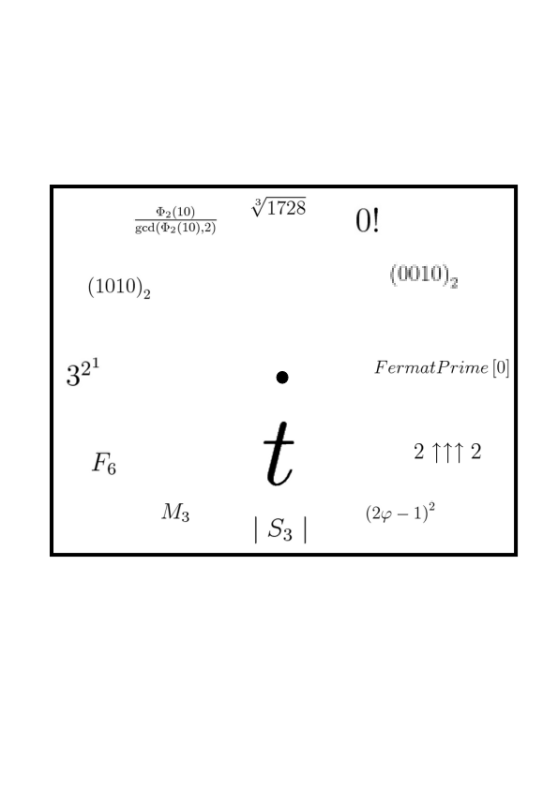
I referred to Wikipedia for the significance of the numbers …..

$\sqrt[3]{1728} = 12$ —- I choose 1728 coz its 1 less than 1729 . The smallest number to represented as a sum of 2 cubes .

$0! = 1$ —- Coz 0! = 1 ….

$\left ( 0010\right )_{10}$ —- 0010 in base 10 is 2 .

$FermatPrime\left[ 0\right ] = 3$ —- 3 is the first Fermat Prime . All numbers satisfying $F_{n} = 2^{2^{ \overset{n} {}}} + 1$

$2 \uparrow\uparrow\uparrow 2 = 4$ —- thats the way 4 represented in Knuth’s Up Arrow Notation .

$\left ( 2\varphi - 1 \right )^2 = 5$ —- where $\varphi$ is the golden ratio $\varphi = \frac{1+\sqrt{5}}{2}$

$\mid S_{3} \mid = 6$ —- 6 is the cardinality of the smallest non-abelian group .

$M_{3} = 7$ —- 7 is the 3 Mersenne Prime .

$F_{6} = 8$ —- 8 is the 6th Fibonacci Number .

$3^{2^{1}} = 9$ —- 9 is an exponential factorial .

$\left ( 1010\right )_2 = 10$ —- 1010 in binary is 10 in decimal (base 10)

$\frac{\Phi_2(10)}{\gcd(\Phi_2(10),2)} = 11^{c} , {c} \in \mathbb{N}$ —- 11 is the second unique prime….

Finally, after the assembly it looked like this ……

a better pic sometime sooner …..

Electoral Polling

Posted on December 23, 2008 by Iceman

Terence Tao has written about electoral polling in a very interesting article here. A non-technical gem from a genius….. 🙂

P.S.:

Try out the assembler game mentioned in the last post . Really interesting.

Added new links : This Week in Evolution which form interesting reading.

Beauty of Numbers

Posted on June 28, 2008 by Iceman

I was stumblingupon sites when i came across something really beautiful . Maybe all of u must be aware of it anyways take a look.

1 x 8 + 1 = 9
12 x 8 + 2 = 98
123 x 8 + 3 = 987
1234 x 8 + 4 = 9876
12345 x 8 + 5 = 98765
123456 x 8 + 6 = 987654
1234567 x 8 + 7 = 9876543
12345678 x 8 + 8 = 98765432
123456789 x 8 + 9 = 987654321

Further….

1 x 9 + 2 = 11
12 x 9 + 3 = 111
123 x 9 + 4 = 1111
1234 x 9 + 5 = 11111
12345 x 9 + 6 = 111111
123456 x 9 + 7 = 1111111
1234567 x 9 + 8 = 11111111
12345678 x 9 + 9 = 111111111
123456789 x 9 +10= 1111111111

Further still…..

9 x 9 + 7 = 88
98 x 9 + 6 = 888
987 x 9 + 5 = 8888
9876 x 9 + 4 = 88888
98765 x 9 + 3 = 888888
987654 x 9 + 2 = 8888888
9876543 x 9 + 1 = 88888888
98765432 x 9 + 0 = 888888888

Finally…

1 x 1 = 1
11 x 11 = 121
111 x 111 = 12321
1111 x 1111 = 1234321
11111 x 11111 = 123454321
111111 x 111111 = 12345654321
1111111 x 1111111 = 1234567654321
11111111 x 11111111 = 123456787654321
111111111 x 111111111=12345678987654321

Louis Posa

Posted on June 5, 2008 by Iceman

This is from a book Mathematical Gems – Ross Honsberger .Its a very famous story of the child prodigy Louis Posa.He was born sometime in the 1940’s and very young attracted the attention of the eminent Hungarian mathematician Paul Erdos.

This is the story of Louis Posa as told by Paul Erdos:

” I will talk about Posa who is now 22 years old and is an author of 8 papers.I met him before he was 12 years old.When I returned from the United States in the summer of 1959 I was told a little oy whose mother was a mathematician and knew quite a bit about high school mathematics.I was very interested a the next day I had lunch with him.While Posa was eating soup I asked him the following question:Prove that if you n+1 integers <= 2n , some pair of them are relatively prime. It is quite easy to see that its not valid for n integers as because no 2 of the n even numbers upto 2n are relatively prime.Actually I discovered this proof some years ago and took about 10 minutes to find a really simple solution.Posa sat there eating his soup and said half a minute later “If you have n+1 integers <= 2n two of them must be consecutive and hence relatively prime.” Needless to say , I was very much impressed, and I venture to class this on the same level as Gauss’ summation of the positive integers upto 100 when he was only 7 years old.From that time onward I worked systematically with Posa.I wrote to him of problems many times during my travels.While still 11 he proved the following theorem which I proposed to him:A graph with 2n vertices and n^2+1 edges must contain a triangle. which he proved at 12 ….” The story goes on…..

Edit : Sorry for the terrible mistake . Thanks to kundor for pointing out the error .